OpenFOAM mint CFD motor

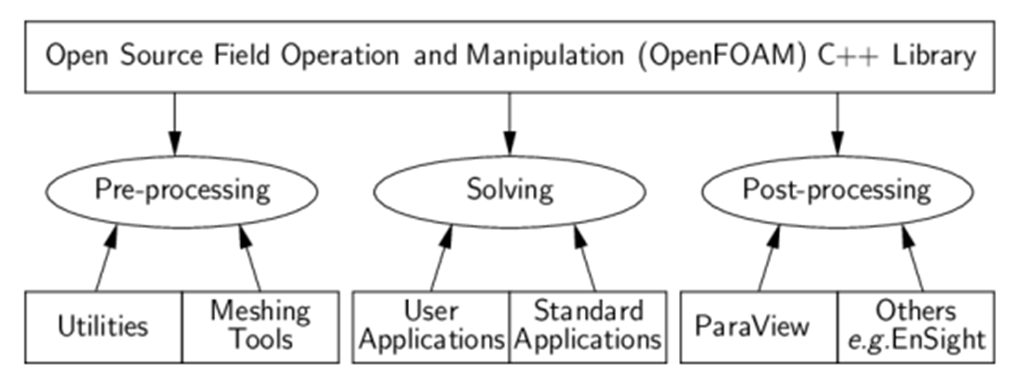
Az OpenFOAM (Open-Source Field Operation and Manipulation) egy erőteljes, nyílt forráskódú számításos áramlástani dinamika (CFD) szoftverkeret. Átfogó numerikus megoldókat és eszközkészletet biztosít a folyadékáramlás, hőátadás és egyéb kapcsolódó jelenségek szimulálására és elemzésére. Az OpenFOAM széles körben használt mind az akadémiai, mind az ipari környezetekben rugalmassága, bővíthetősége, valamint a felhasználók számára lehetőséget biztosító új megoldók és modellek testreszabásának képessége miatt.

Az OpenFOAM a GNU General Public License (GPL) alatt kerül kiadásra, így szabadon elérhető a használatra, módosításra és terjesztésre. Ez a nyílt forráskódú jelleg ösztönzi az együttműködést és az innovációt a CFD közösségen belül. A szoftver moduláris architektúrával rendelkezik, amely lehetővé teszi a felhasználók számára, hogy hozzáadjanak vagy módosítsanak összetevőket az egyedi igényeiknek megfelelően. Új megoldók, határfeltételek, turbulenciamodellek és egyéb funkciók fejleszthetők és zökkenőmentesen integrálhatók a rendszerbe. Az OpenFOAM hálózatosítási lehetőségeket kínál, amelyekkel a felhasználók bonyolult, strukturált és strukturálatlan hálókat generálhatnak a szimulációkhoz. Emellett számos turbulenciamodellt tartalmaz, kezdve a standard k-epsilon és k-omega modellektől egészen a fejlettebb Large Eddy Simulation (LES) és Direct Numerical Simulation (DNS) módszerekig, és széles körű beépített megoldókat kínál különféle folyadékáramlási és hőátadási problémák megoldására. Ezek közé tartoznak a laminaris és turbulens áramlások, kompresszibilis és inkompresszibilis áramlások, többfázisú áramlások és egyéb problémák megoldására szolgáló megoldók.

Bemeneti paraméterek és határfeltételek

Az áramlástani dinamika alapvető egyenleteit diszkretizálják és numerikusan oldják meg egy háromdimenziós térbeli régióban, amely magában foglalja az építészeti szerkezetet, és amelyet számítási tartománynak neveznek. Ezt a tartományt határoló hat felszín jellemzi, amelyek jellemzően egy téglatest formát alkotnak. Ezen határoló felületek, a tartomány alján kívül, nem rendelkeznek közvetlen fizikai megfelelővel, ami eltéréseket okoz a valós világban előforduló körülményektől. Ezek az eltérések hibákat vezetnek be az áramlás szimulációjában, amelyeket "tartományhibáknak" neveznek. A hibák csökkentése érdekében elengedhetetlen, hogy ezeket a nem fizikai határoló felületeket kellő távolságra helyezzük az építészeti struktúrától, így minimalizálva azok hatását az áramlás viselkedésére. Azonban ezen határok túlzott eltávolítása növelheti a modell számítási terhét. Ezért a számítási tartomány mértékét bölcsen kell meghatározni, figyelembe véve mind a számítási hatékonyságot, mind a megoldások pontosságát.

A számítási szélmérnökség elvei, amelyeket jól bevált irányelvek szabályoznak, hangsúlyozzák a számítási tartomány megfelelő méretezésének kulcsfontosságú szerepét a megoldás pontosságának biztosítása érdekében. Ezek az irányelvek kapcsolatot létesítenek a tartomány konfigurációjából eredő hibák és a szélcsatornás kísérletekben tapasztalható hasonló problémák, mint például a blokkolási hatások között, amelyek akkor jelentkeznek, ha a tartomány keresztmetszeti területei korlátozottak, illetve a helyi áramlási jelenségek mesterséges felerősödésében, amikor nem elegendő tér áll rendelkezésre a tartomány határai és az építészeti modell között. Ennek következményeként a tartományhatárok és az építészeti modell közötti minimális távolság meghatározása, valamint a maximális blokkolási arányok vagy mindkét tényező szinergikus kombinációja szükséges a megfelelő tartományméret meghatározásához.

Háló generálási folyamatok

A háló generálásának folyamata jellemzően két alapvető szakaszból áll: a számítási tartomány diszkretizálásából és a vizsgált szerkezet beillesztéséből ebbe a tartományba.

Ehhez az OpenFOAM két kulcsfontosságú eszközt alkalmaz: a „blockMesh” és a „snappyHexMesh” eszközöket. Ezek az eszközök kulcsszerepet játszanak a strukturált és nem strukturált rácsok létrehozásában, lehetővé téve a bonyolult áramlástani jelenségek pontos szimulációját.

A blockMesh elsősorban strukturált rácsok generálására szolgál. Ez egy strukturált derékszögű koordináta rendszert alkalmaz, amely lehetővé teszi ortogonális hexaéderes cellák létrehozását, ezzel egyszerűsítve a parciális differenciálegyenletek numerikus megoldását. Az eszköz úgy működik, hogy a számítási tartományt blokkokra osztja, majd ezeket a blokkokat további cellákra bontja a csúcsok és élek meghatározásával. A blokk topológia, valamint a határfeltételek és a cella finomítások egy szótárfájlban vannak meghatározva a blockMesh utility végrehajtása előtt. Ez a megközelítés különösen jól alkalmazható egyszerűbb geometriák esetén, ahol a derékszögű rács struktúrája világos ábrázolást ad a tartományról.

Ezzel szemben a snappyHexMesh akkor alkalmazandó, ha bonyolultabb geometriákkal találkozunk, amelyek nem strukturált rácsokat igényelnek a jobb pontosság és rugalmasság érdekében. Ez az eszköz a „snap” koncepciójára épít, amely az alapsóháló deformálását jelenti, hogy illeszkedjen a vizsgált geometria felületéhez.

Ezért a háló generálási folyamat a következő szakaszokból áll:

• Háttér Háló Generálás: Egy kezdeti rács generálódik, amely háttérrácsként működik, és lefedi az egész számítási tartományt.

• Geometria Előkészítés: A célgeometria előkészítése egy meghatározott formátumban, amely tartalmazza a felületi leírást és a vonatkozó finomítási paramétereket.

• Háló „Snap” alkalmazás: A kezdeti háttérrács deformálódik, vagyis „snappelik” a geometria felületére iteratív algoritmusok alkalmazásával. Ez biztosítja, hogy a háló pontosan illeszkedjen a bonyolult alakhoz.

• Cella Rétegek Hozzáadása: A felület illesztése után egy prizmás vagy hexaéderes cellákból álló réteg adható hozzá a geometria felületéhez, hogy rögzítse a határréteg hatásait.

• Háló Finomítás: Helyi hálófinomítások alkalmazhatók az érdeklődési területeken, biztosítva a magasabb hálófelbontást ott, ahol szükséges.

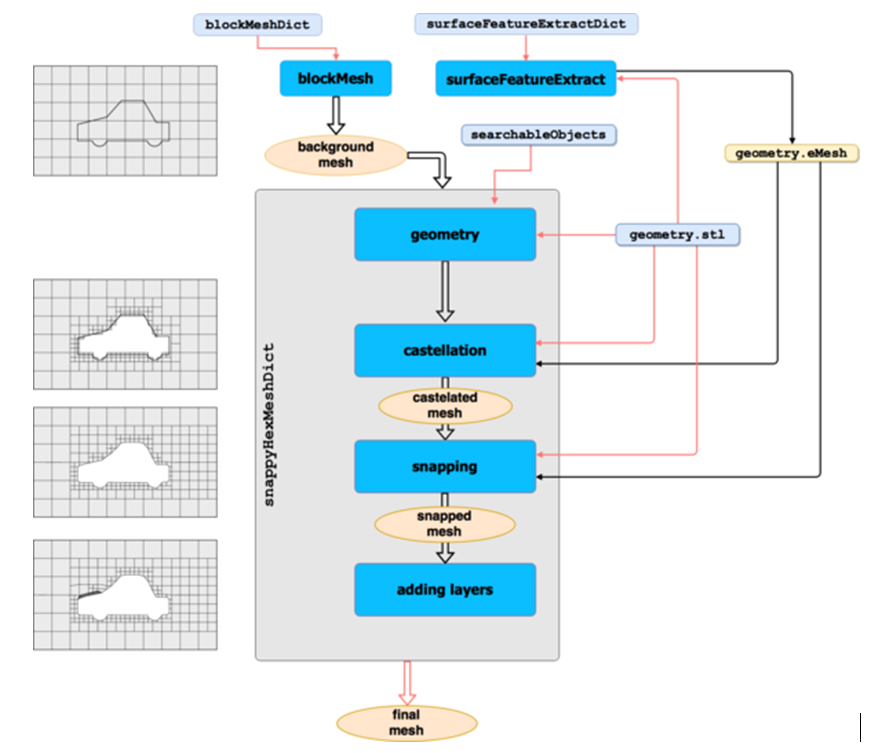The overview of the meshing procedure via OpenFOAM

Turbulencia modellezés

A turbulencia modellezése alapvető része a Számított Folyadékdinamika (CFD) szimulációknak, amelyeket a különböző mérnöki alkalmazásokban a folyadékáramlások viselkedésének előrejelzésére használnak. A turbulencia a magas sebességek mellett térben és időben bekövetkező kaotikus változásokat jelenti, ami egy olyan jelenség, amelyet nehéz pontosan modellezni és előre jelezni a hagyományos módszerek alkalmazásával. A CFD szimulációk célja a bonyolult kölcsönhatások és ingadozások megragadása, amelyek a turbulens áramlásokban jelentkeznek, különböző turbulencia modellek alkalmazásával.

A valóságos környezetekben a turbulencia mindenhol jelen van, és jelentős hatással van a folyadék viselkedésére, hőátadásra és anyagtranszportra.

A turbulencia hatásainak pontos előrejelzése kulcsfontosságú az olyan mérnöki rendszerek tervezésében, mint a repülőgépek, járművek, épületek és ipari folyamatok, mivel ezek hatással vannak a rendszer teljesítményére és biztonságára. Azonban a turbulencia közvetlen szimulálása azt jelenti, hogy a Navier-Stokes egyenleteket minden egyes turbulens örvényre meg kell oldani, ami számítási szempontból nem praktikus a legtöbb alkalmazás esetén. A turbulencia modellek egy kompromisszumot kínálnak a pontosság és a számítási költség között.A turbulencia modellezése alapvető része a Számított Folyadékdinamika (CFD) szimulációknak, amelyeket a különböző mérnöki alkalmazásokban a folyadékáramlások viselkedésének előrejelzésére használnak. A turbulencia a magas sebességek mellett térben és időben bekövetkező kaotikus változásokat jelenti, ami egy olyan jelenség, amelyet nehéz pontosan modellezni és előre jelezni a hagyományos módszerek alkalmazásával. A CFD szimulációk célja a bonyolult kölcsönhatások és ingadozások megragadása, amelyek a turbulens áramlásokban jelentkeznek, különböző turbulencia modellek alkalmazásával.

A valóságos környezetekben a turbulencia mindenhol jelen van, és jelentős hatással van a folyadék viselkedésére, hőátadásra és anyagtranszportra.

A turbulencia hatásainak pontos előrejelzése kulcsfontosságú az olyan mérnöki rendszerek tervezésében, mint a repülőgépek, járművek, épületek és ipari folyamatok, mivel ezek hatással vannak a rendszer teljesítményére és biztonságára. Azonban a turbulencia közvetlen szimulálása azt jelenti, hogy a Navier-Stokes egyenleteket minden egyes turbulens örvényre meg kell oldani, ami számítási szempontból nem praktikus a legtöbb alkalmazás esetén. A turbulencia modellek egy kompromisszumot kínálnak a pontosság és a számítási költség között.

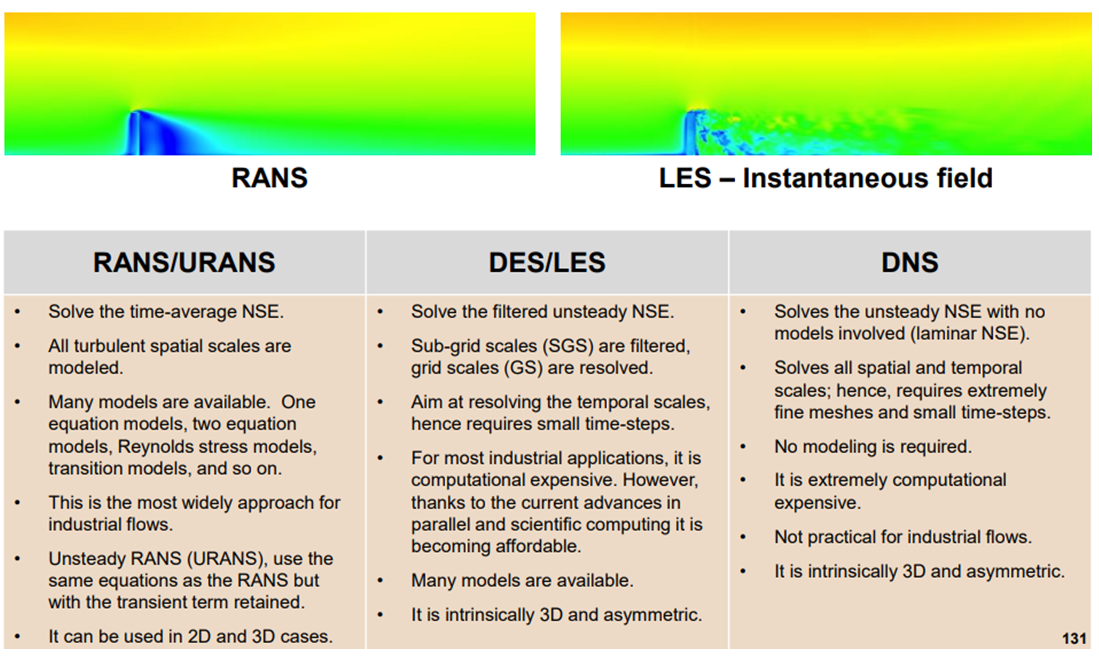Overview of turbulence modelling approaches

A turbulencia modellek két fő típusra oszthatók: a Reynolds-átlagolt Navier-Stokes (RANS) modellekre és a Nagy Örvény Szimuláció (LES) modellekre. A RANS modellek az áramlási változókat időben és térben átlagolják, hogy megkapják az átlagos áramlási tulajdonságokat. Ezek a modellek az átlagos áramlási mezőt oldják meg, miközben további egyenleteket adnak meg a turbulens ingadozások előrejelzésére. Ezzel szemben az LES modellek kifejezetten a nagyobb örvényeket szimulálják, miközben a kisebb örvények modellezését végzik. Ez a megközelítés számítási szempontból nagyobb igényeket támaszt, mint a RANS modellek, de nagyobb pontosságot biztosíthat bonyolult áramlások esetén. Az LES alkalmas a nagyméretű turbulens struktúrák megragadására.

A megfelelő turbulencia modell kiválasztása számos tényezőtől függ, mint például az áramlás típusa, a geometriai összetettség, a számítási erőforrások és a kívánt pontosság. Az egyszerű áramlások, jól meghatározott geometriákkal, előnyös helyzetben lehetnek a RANS modellekkel a hatékonyságuk miatt, míg a bonyolult, időben változó áramlásokhoz az LES szükséges a pontos előrejelzésekhez.

A turbulencia modellezése nem mentes a kihívásoktól. A modellek gyakran empirikus konstansokra támaszkodnak, amelyek nem minden esetben alkalmazhatók univerzálisan. Néhány áramlás, különösen azok, amelyek elválással, sokk hullámokkal vagy időben változó jelenségekkel kapcsolatosak, kihívást jelenthetnek a turbulencia modellek pontosságában. Az alkalmazott rács felbontás és a határfeltételek szintén kulcsszerepet játszanak az értelmes eredmények elérésében.

Összefoglalva, a turbulencia modellezés a CFD szimulációk egyik alapvető aspektusa, amely összeköti a számítási lehetőségeket és a turbulens áramlások pontos előrejelzését. A megfelelő modell kiválasztása és annak korlátainak megértése kulcsfontosságú ahhoz, hogy megbízható betekintést nyerjünk a bonyolult folyadékviselkedésbe.

A legszélesebb körben használt turbulencia modell a k-epsilon RANS modell. Célja a turbulens áramlás tulajdonságainak előrejelzése, elsősorban a turbulens kinetikus energia (k) és a turbulens disszipációs sebesség (ε) meghatározása. E két mennyiség alapvető a turbulencia áramlási mezőbeli jellemzésében. Íme egy rövid magyarázat a k-epsilon modellről:

• Turbulens kinetikus energia (k): A turbulens áramlások különböző méretű örvényekből és örvényekből állnak. A turbulens kinetikus energia azt az energiát jelenti, amely a turbulens örvényekhez kapcsolódik.

• Turbulens disszipációs sebesség (epsilon): Ez az az ütem, amelynél a turbulens kinetikus energia hővé alakul a viszkozitás disszipációja következtében. A sebesség a sebesség-ingadozások gradiensének figyelembevételével számítható.

A k-epsilon modell a k és ε szállítási egyenleteit oldja meg, figyelembe véve a turbulencia termelésére, disszipációjára és turbulens diffúziójára ható tényezőket. A modell a lokális egyensúly feltételezésére épít, ami azt jelenti, hogy a turbulens termelés és disszipáció minden egyes áramlási pontban egyensúlyban van.

A k-epsilon modell viszonylag egyszerű és számítási szempontból hatékony, ezért népszerű választás a mérnöki szimulációk széles spektrumában. Azonban nem biztos, hogy pontosan megragadja bizonyos turbulens áramlások komplexitásait, különösen azokat, amelyek erős örvénylő vagy anizotróp viselkedést mutatnak. Ilyen esetekben előnyösebb lehet a fejlettebb turbulencia modellek alkalmazása, mint például a Reynolds Stress Model (RSM) vagy a Nagy Örvény Szimuláció (LES). A turbulencia modell kiválasztása az áramlás jellegétől és a kívánt pontosságtól függ.

Számoldó algoritmusok

A számításos folyadékdinamika (CFD) solvers kulcsfontosságú elemei a numerikus szimulációknak, amelyek lehetővé teszik a folyadék áramlásának és a szilárd struktúrákkal való kölcsönhatások tanulmányozását és elemzését. Ezek a solvers különböző matematikai és számítástechnikai technikákat alkalmaznak, és képesek szimulálni az összetett folyadékdinamikai forgatókönyveket, amelyek fizikális kísérletekkel nehezen vagy egyáltalán nem tanulmányozhatók.

A CFD solvers úgy működnek, hogy a folyadék mozgásának irányító egyenleteit (Navier-Stokes egyenletek) numerikus rácsba vagy hálóba diszkrétálják, amely átfogja a számított teret. Ez a háló diszkrét cellákból vagy elemekből áll, ahol a folyadék tulajdonságait számolják és frissítik az egyes diszkrét időpontokban. A választott solver függ az áramlás típusától, a szükséges pontosságtól és a rendelkezésre álló számítási erőforrásoktól.