Analízis típusok

Rugalmas analízis

Elsőrendű analízis

Az elsőrendű analízis a szerkezete kezdeti merevsége alapján számítja ki a szerkezet alakváltozásait, igénybevételeit. A modell elkészülte után ajánlatos először elsőrendű analízist futtatni és ez alapján leellenőrizni a szerkezet viselkedését, mielőtt időigényesebb számítást futtatnánk (például sajátérték számítás). Az elsőrendű számítás végrehajtásának lépései a következők:

1. A végeselem elsőrendű (kezdeti) merevségi mátrixának számítása lokális koordináta rendszerben
2. A teljes szerkezet globális merevségi mátrixának ($K_s$) és erővektorának ($P$) előállítása, az elem merevségi mátrixok globális koordináta rendszerbe történő transzformálásával
3. A globális merevségi mátrix és az erővektor módosítása a peremfeltételek figyelembevételével (támaszok, rúdvégi folytonosság, előírt elmozdulás, hőmérsékletteher stb.)
4. Az alkalmazott csomóponti erők – a terhekből előállított ismert változó – és a csomóponti elmozdulások – ismeretlen változó ($U$) – közötti kapcsolatot leíró lineáris egyenletrendszer megoldása a szerkezet globális koordináta rendszerében a globális modellre (a csomóponti elmozdulások és erők értelmezését, lásd Végeselemek fejezetben.):

$K_sU=P \rightarrow U=K_{s}^{-1}P$

(1)

5. Az elemek igénybevételeinek (és feszültségeinek) ($f^{el}$) számítása a lokális koordináta rendszerekben, az elemek globális csomóponti elmozdulásainak lokális merevségi mátrixszal lokális koordináta rendszerekbe ($u^{el}$) való transzformálásával:

$f^{el}=K_s^{el}u^{el}$

(2)

Másodrendű számítás

A másodrendű számítás figyelembe veszi, hogy a terhelt és deformált szerkezet a terhelés hatására eltérően viselkedik, mint az elsőrendű számításnál. Ez a hatás a kezdeti merevség terhelés hatására létrejövő változásaként vehető figyelembe. A másodrendű számítás lépései:

1. Az elsőrendű számítás fentiekben leírtak szerinti végrehajtása
2. A végeselemek geometriai merevségi mátrixának ($K_g^{el}$) saját koordinátarendszerben történő meghatározása az egyes elemek igénybevételeinek ($f^{el}$) figyelembevételével
3. A másodrendű globális merevségi mátrix ($K_s+K_g$) és a teljes modell erővektorának ($P$) előállítása, az elem merevségi mátrixok globális koordináta rendszerbe történő transzformálásával
4. A globális másodrendű merevségi mátrix és az erővektor módosítása a peremfeltételek figyelembevételével (támaszok, rúdvégi folytonosság, előírt elmozdulás, hőmérsékletteher stb.)
5. Az alkalmazott csomóponti erők – a terhekből előállított ismert változó – és a csomóponti elmozdulások – ismeretlen változó ($U$) – közötti kapcsolatot leíró lineáris egyenletrendszer megoldása a szerkezet globális koordináta rendszerében a terhelt és deformált globális modellre (a csomóponti elmozdulások és erők értelmezését lásd, a Végeselemek fejezetben):

$(K_s+K_g)U=P \rightarrow U=(K_s+K_g)^{-1}P$

(3)

6. Az elemek igénybevételeinek (és feszültségeinek) ($f^{el}$) számítása a lokális koordináta rendszerekben, az elemek globális csomóponti elmozdulásainak lokális merevségi mátrixszal lokális koordináta rendszerekbe ($u^{el}$) való transzformálásával:
   $f^{el}=K_s^{el}u^{el}$
7. Ha egy csomóponti korábbi helyzethez viszonyított elmozdulása egy határértéket túllép, akkor a számítás a második lépéstől ismétlődik.

Statikai sajátérték – kihajlás analízis

A sajátértékszámítás mechanikai értelmezése egy olyan rugalmas kritikus terhelési szint, amelynél a szerkezet valamilyen módon elveszíti a stabilitását. Matematikailag ez azt jelenti, hogy a másodfokú egyenletnek (3) nincs megoldása, mert a másodrendű merevségi mátrix szinguláris. A Consteel programban a lineáris sajátérték számítás egy paramétert vesz figyelembe, a konzervatív terhelés és a geometriai merevségi mátrix a teherfaktortól (λ) lineárisan függ:

$K_g(\lambda f)=\lambda K_g(f)$

(4)

Ebben az esetben a sajátérték számítás az alábbi formában írható fel:

$(K_s+\lambda K_g)U=0$

(5)

Az egyenletnek a megoldásai a kritikus teherfaktorok (kihajlási teher faktor $\lambda_{cr}^i$) amelyek a másodrendű merevségi mátrixokat szingulárissá teszik és az elmozdulások (kihajlási alakok $U^i$).

A sajátérték analízis elvégzésével kapott lehetséges kihajlási alakokat alapvetően befolyásolja a figyelembe vett másodrendű hatás, amit az alkalmazott végeselem típus határoz meg. Például 7 SZF oszlop-gerenda végeselem esetén figyelembe vehető az összes globális kihajlási alak: kihajlás, elcsavarodó kihajlás, kifordulás és ezek interakciója.

Kihajlási érzékenységi vizsgálat

Ezen funkció segítségével összefoglaló képet kapunk a szerkezet kihajlási alakjairól, illetve rudanként megadja, hogy az adott rúd stabilitás vizsgálatához melyik teherkombináció melyik kihajlási alakja a legrelevánsabb, azaz melyiket érdemes alkalmazni. A későbbi globális méretezés (ld. Globális vizsgálatok) során ez alapján a program automatikusan ki tudja választani a megfelelő kritikus teherfaktort.

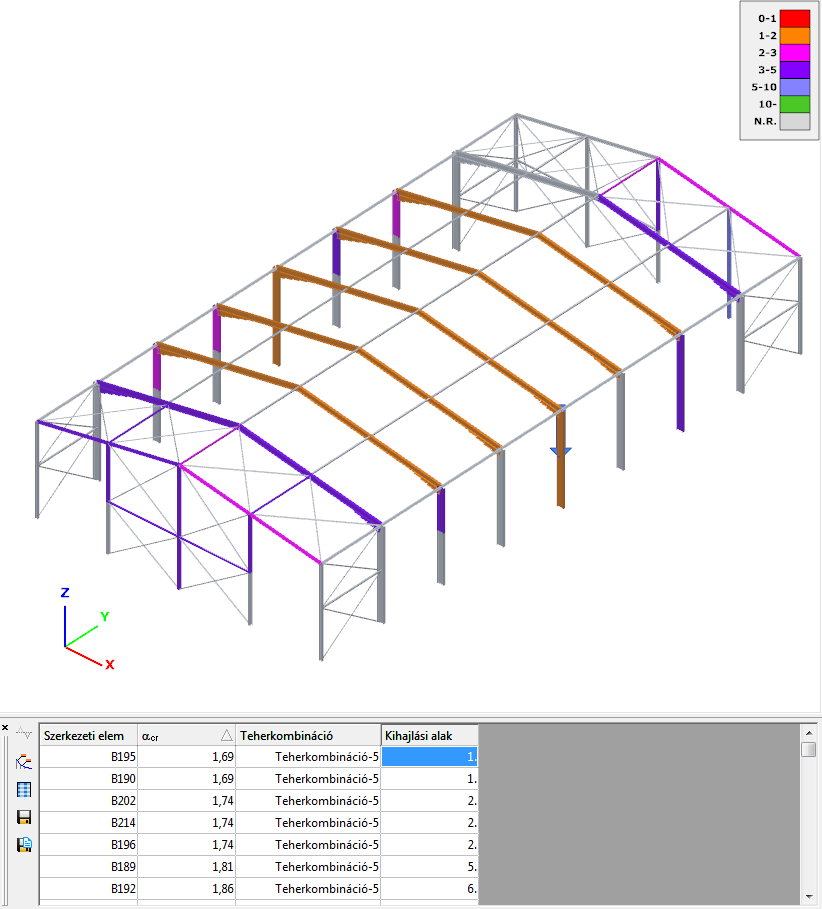
Imperfekciós érzékenységi vizsgálat

Az imperfekciós érzékenységi vizsgálat segítségével minden stabilitásvesztési alakhoz meghatározható a kritikus rúdelem és kritikus pont (ekvivalens pont), ami alapján az imperfekciós alak amplitúdója számolható. A grafikus ábrán a stabilitásvesztési alakot imperfekciós elmozdulás-teherként alkalmazva kapott igénybevételekből, feszültség alapon számított kihasználtságok láthatók minden, ahol a legnagyobb kihasználtsághoz tartozó keresztmetszet kapja a 100% értéket. ld. még a Globális imperfekciók fejezetet.

Dinamikai sajátérték – rezgésanalízis

A dinamikus sajátérték számítás mechanikai értelmezése a szerkezet sajátfrekvenciáinak meghatározása. A lineáris sajátérték analízis elvégzése során a Consteel a másodrendű merevségi mátrixot és a konzisztens tömeg mátrixot (M) veszi figyelembe.

$((K_s+K_g)+\omega^{2}M)U=0$

(6)

Az egyenletnek a megoldásai a sajátfrekvenciák ($omega^i$) és az elmozdulások (szabad rezgési alakok $U^i$).

A sajátérték analízis elvégzésével kapott lehetséges rezgési alakokat alapvetően befolyásolja a figyelembe vett merevség és tömeg mátrix, amit az alkalmazott végeselem típus határoz meg. Például 7 SZF oszlop-gerenda végeselem esetén figyelembe vehető az összes globális rezgési alak: kihajlás, elcsavarodó kihajlás, kifordulás és ezek interakciója.

Képlékeny analízis

Képlékeny analízis indítására az Analízis fül Analízis beállításai ablakon van lehetőség. Ehhez a Számítás típusa legördülő menü, Képlékeny opció kiválasztására van szükség.

Alapok

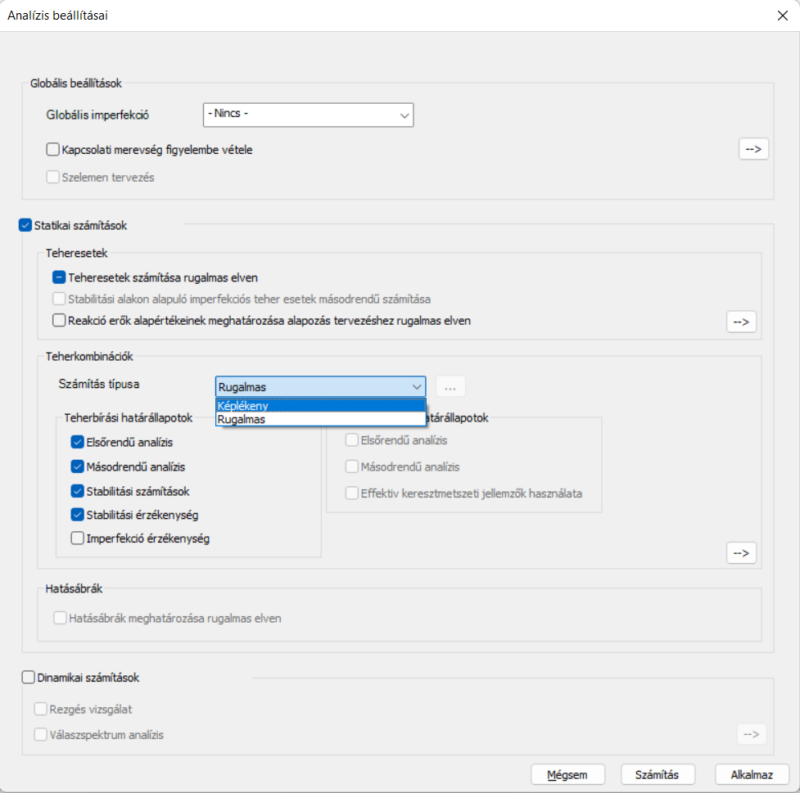
Képlékeny analízis választása esetén, képlékeny csukló analízis fut le, amely figyelembe veszi a kizárólag erőstengely körül nyomaték (My) hatására, a keresztmetszet y lokális tengelye kerül kialakuló síkbeli képlékeny csuklókat – más hatásnak (nyírás, normálerő vagy gyengetengely körüli hajlítás) nincs hatása a csuklók kialakulására. Az analízis beállításai elérhetők az Analízis beállításai dialógon, a Számítás típusa legördítő menü mellett található három pontos () ikonra kattintva.

Az első csoportban a képlékeny csuklók kialakulásának feltételei állíthatók be. A legördülő menü segítségével kiválasztható részmodell is. Ebben az esetben az analízis a képlékeny csuklókat csak a kiválasztott részmodellben fogja keresni. Keresztmetszetek tekintetében két opció érhető el, ahol a képlékeny csuklók kialakulhatnak: keresztmetszetek minimum egyszeresen szimmetrikusak (a lokális z tengely körül) és kompakt (AISC szabvány esetén) vagy első osztályú (EuroCode szabvány esetén). A szokásos szabványos előírásoknak megfelelően ennek a két feltételnek szükséges teljesülnie képlékeny analízis végrehajtásához. A képlékeny csukló analízis pontossága is megadható a képlékeny nyomatéki ellenállás százalékában (Mpl).

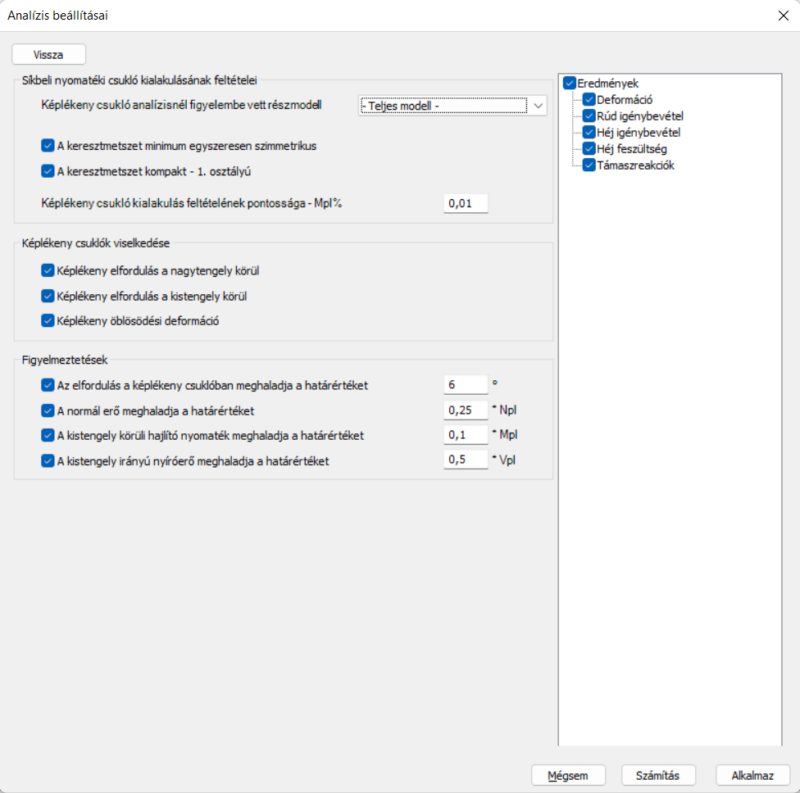
A második csoportban a képlékeny csuklók kialakulása utáni mechanikai viselkedése állítható be. Mivel a síkbeli (síkbeli kifejezés csak a csukló kialakulására vonatkozik) csuklók részei egy térbeli modellnek, ezért meg kell határozni a kialakulás utáni térbeli mechanikai viselkedésüket (térbeli csukló). Ennek megfelelően a kialakult csuklók el tudnak fordulni az erős tengely körül, illetve a gyenge tengely körül a szabad öblösödési deformációval együtt. A két utóbbi opció segítségével realisztikusan figyelembe vehető, hogy a képlékeny csuklók okozta teljes övmegfolyások egy I szelvény esetén gyakorlatilag kistengely körüli és öblösödési csukló viselkedést tesznek lehetővé. Ezek az opciók befolyásolják a síkra merőleges viselkedését a modellnek (például abban az esetben, ha egy szerkezeti elem kihajlása a képlékeny csukló mellett alakul ki a csukló síkjára merőlegesen).

A harmadik csoportban található beállítási lehetőségek segítségével különböző figyelmeztetéseket megjelenítésére van lehetőség az analízis során. A figyelmeztetések abban az estben jelennek meg, ha a képlékeny csuklók kialakulására jelentős hatással bír a nagytengely körüli hajlításon kívül más igénybevétel is.

A negyedik csoportban adható meg, hogy mely analízis eredmények kerüljenek elmentésre és megjelenítésre minden egyes státuszban. Nagy modell és jelentősszámú képlékeny csukló esetén az eredmény mérete jelentős lehet, ezért tanácsos csak azokat az eredmény típusokat kiválasztani, amelyekre ténylegesen szükség van.

Elsőrendű analízis

Matematikailag a rugalmas számításnál leírtakhoz hasonlóan történik, de azzal a nagy különbséggel, hogy nem csak a megadott terhelésre végez analízist, hanem a megadott terhelést lépésenként addig változtatja (növeli vagy csökkenti), amíg a szerkezet instabillá nem válik a kialakuló képlékeny csuklók miatt.

A megoldás folyamata a következő:

1: A felhasználó által megadott teherkombinációnak megfelelően lefut egy elsőrendű rugalmas analízis, majd a kapott erős tengely körüli My hajlítónyomaték értékek az első csoportban szereplő szempontok szerint összehasonlításra kerülnek a végeselemhez rendelt szelvény képlékeny nyomatéki ellenállásával.

2a: Amennyiben a képlékeny analízisre kijelölt elemek egyetlen pontjában sem érik el a felhasználó által megadott teherszinten számolt igénybevételek a képlékeny csukló(k) kialakulásának feltételeit, a Consteel a teherszintet lépésekben emeli mindaddig, amíg az első képlékeny csukló ki nem alakul.

2b: Amennyiben a felhasználó által megadott teherszinten van olyan pont, ahol a képlékeny csukló kialakulna, a Consteel a teherszintet lépésekben csökkenti addig a teherszintnek a megtalálásáig, amikor az első képlékeny csukló kialakulna.

3: A megtalált $(\alpha *MyEd)$ teherszinten az aktuális összes olyan végeselempontra, ahol a képlékeny csukló kialakulásának a feltételei adottak, a Consteel csuklót helyez el a „Képlékeny csuklók viselkedése” paramétereknek megfelelően, amely a további teherlépcsőkre elvégzett analízisnél kerül alkalmazásra. Az csuklók elhelyezése miatt a szerkezet globális merevségi mátrixa aktualizálásra kerül és egy újabb számítási szint indul. Az elhelyezett csuklók grafikusan ábrázolásra kerülnek majd következő számítási lépés indul.

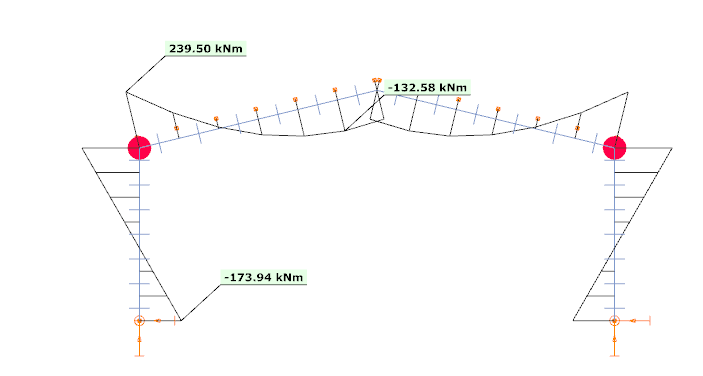
4: A Consteel tovább növeli a terhelést az α teherszorzón keresztül, a megváltoztatott merevségi mátrix használatával mindaddig, amíg a következő képlékeny csukló kialakulásának a teherszintjét el nem éri.

5: A 3. ponthoz hasonlóan elhelyez csuklókat az újonnan megtalált csomópontokra, aktualizálja a merevségi mátrixot és folytatja az iterációt a 4. pont szerint.

A képlékeny analízis akkor ér véget, amikor a kialakuló képlékeny csuklók eredményeképpen a szerkezet instabillá változik. Amennyiben az így kapott végső teherszorzó értéke 1.00 alatti, a szerkezet instabil és az elsőrendű számítás eredmény nélkül záródik. Erre üzenet figyelmezteti a felhasználót.

Az iteráció során, amikor a program eléri az 1.00 teherszorzó értéket, az aktuális igénybevétel értékek elmentődnek, mert a teherbírás vizsgálatokat ezen a szinten – azaz a megadott terhelések szintjén – kell elvégezni. Ezek az igénybevételek lesznek az alapjai a további lépésben elvégzendő sajátérték-kihajlás analízisnek.

Az egyes teherszint-növelési lépések, a hozzá tartozó teherszorzók és a lépés során kialakult képlékeny csuklók története végig nézhető az analízis típusok legördülő menüben megjelenő „Képlékeny csuklók” opció választásával.

Másodrendű analízis

Hamarosan!

Statikai sajátérték – kihajlás analízis

Az elsőrendű analízisnél leírt iterációt végzi a program az 1,00 teherszorzó értékig, ami a megadott teherszintnek felel meg. Az ezen a teherszinten érvényes statikai váznak megfelelő elsőrendű Ks és az ehhez tartozó igénybevételeloszláshoz számolt Kg mátrixok használatával a rugalmas számításnál leírtak szerint történik a számítás.