Végeselemek
Alapok
A mechanikai eredmények és a számítás korlátai nagyban függenek a számított modellben alkalmazott végeselemek típusától. Az analízis minőségét, a várható eredményeket és ezzel összhangban az alkalmazható szabványos ellenőrzéseket, a figyelembe vett elmozdulások, erők, keresztmetszeti funkciók és másodrendű hatások határozzák meg. Annak érdekében, hogy a mérnök a szerkezet „működését” a lehető legpontosabban meghatározhassa, és hogy elkerülje a szerkezet nem várt viselkedését, a mérnöknek a modellezés során ügyelnie kell az egyes alkalmazott végeselemek jellemzőire. A Consteel programban minden végeselemes modell a tényleges 3D-ben működik; nincs mód a szabadságfokok korlátozására (síkbeli keret stb.). Ha szükséges, támaszok és/vagy teherrendszerek alkalmazásával megoldható. Az összes teher és támasz, teheresetenként csomóponti erőkké és csomóponti támasszá kerülnek konvertálásra, végeselem mentén megoszló erő és támasz nem alkalmazható. A konvertálást a végeselem generálás során automatikusan végzi a program.
A következő fejezet nem törekszik az alkalmazott végeselemeket megalapozó elméletek bemutatására, mert ezek a szakirodalmakban megtalálhatók. Mindössze azokat a tulajdonságokat mutatja be, amelyek ismerete az eredmények helyes értelmezéséhez szükségesek.
Vonalelemek
Három végeselem típus használható:
- 6 szabadságfokú (6SZF) általános elem, olyan rudak modellezésére, amelyeken tengelyirányú erő, nyíróerő, nyomaték, csavarás vagy ezek tetszőleges interakciója működik
- 7 szabadságfokú (7SZF) rúdelem öblösödéssel elem, működése megegyezik a 6SZF elemmel, kiegészítve az öblösödés hatásával
- húzott rúd (HR) elem, olyan 1 szabadságfokú rudak modellezésére, amelyek nyomást nem tudnak felvenni
6 szabadságfokú rúdelemet használ a Consteel a vasbeton elemek és öszvér gerendák modellezésére. A Consteel által alkalmazott 6 szabadságfokú rúdelem a nyírási alakváltozásokat is figyelembe tudja venni.
A 7SZF elem speciálisan olyan vékonyfalú rudakhoz került kifejlesztésre, ahol a keresztmetszet öblösödésének figyelembevétele különösen fontos a viselkedés során. Ez a hatás jelenik meg a hetedik szabadságfokban. A következő ábra bemutatja a csomóponti elmozdulásokat:
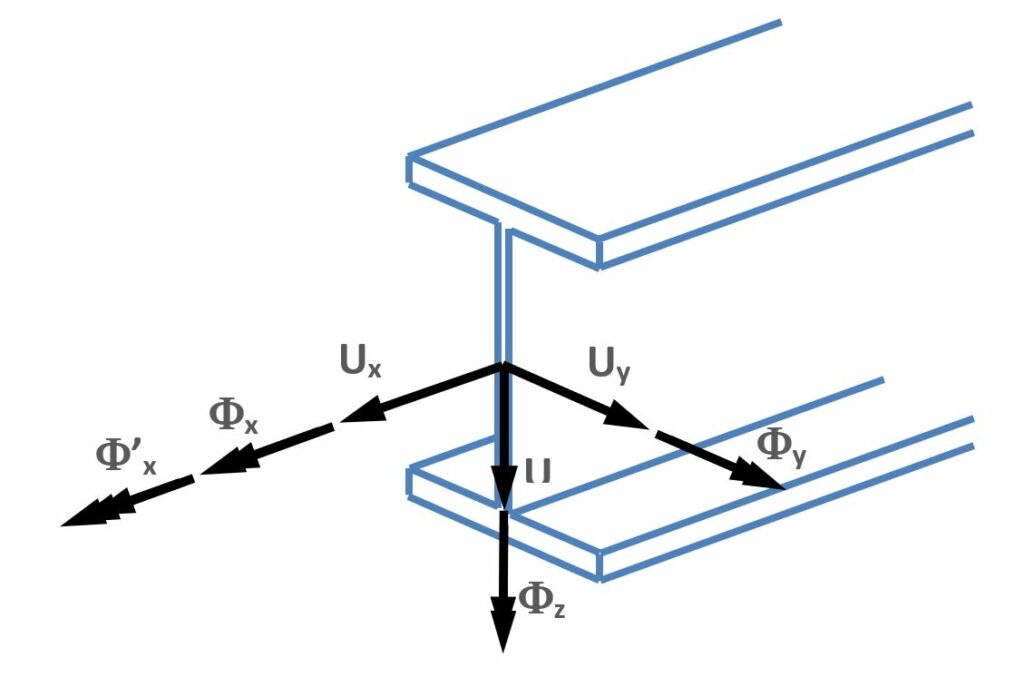
Az első 6 SZF a hagyományos elmozdulásokat (Ux, Uy, Uz) és elfordulásokat (Fx, Fy, Fz) tartalmazza, a rúd helyi koordinátarendszerében (lásd Koordináta rendszerek). A hetedik szabadságfok több magyarázatot igényel. Ez szabadságfok a hossztengely menti elfordulás első deriváltját (F'x) jelenti matematikailag, mechanikailag a szelvény öblösödését jelenti, amely egyenes következménye a vékonyfalú szelvény torzulásának. Az alábbi ábra az öblösödést igyekszik bemutatni. Az öv kilép a szelvény eredeti síkjából.
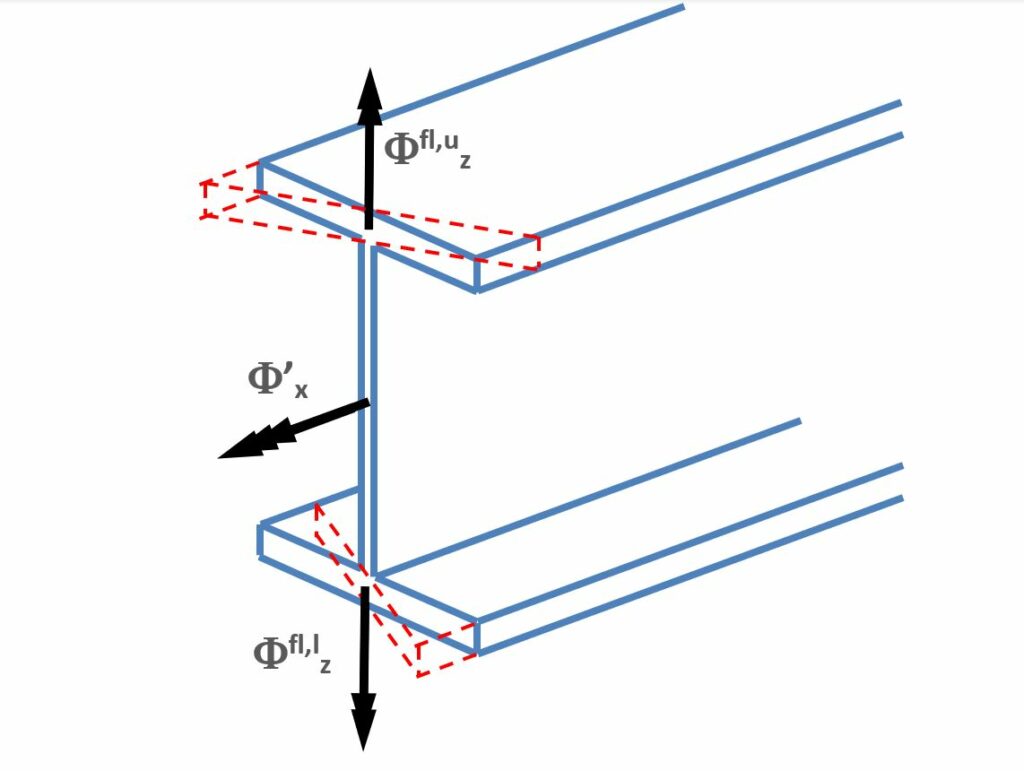
Ebben az esetben az öblösödés szabadságfoka, mint két, ellentétes irányú az öv tengelyére merőleges tengely körüli elfordulásként értelmezhető.
A 7 szabadságfokú rúdelemnek egy speciális továbbfejlesztett változatát használja a Consteel lineárisan változó keresztmetszetű rudak modellezésére.
Mivel az acél szelvényű rudak általában karcsúak, ezért globális stabilitásvesztésüknek számos változata fordulhat elő: kihajlás, elcsavarodó kihajlás, kifordulás, és ezek együttes hatása. A 7 SZF végeselemeknek köszönhetően mindezen módok számíthatók. Ilyen rudak stabilitásszámításakor ez egy fontos és előnyös lehetőség, de mivel a komplex elcsavarodások pontos számítása nagyban függ a 7. öblösödési szabadságfoktól, ennek hatását már a modell felépítésénél figyelembe kell venni (lásd a Szerkezet modellezése fejezet figyelmeztetéseit).
A húzott rudak (HR) csak akkor szerepelhetnek az első- és másodrendű analízisben, ha húzásnak vannak kitéve. Ennek megfelelően a számítás iteratív, ha HR elemek vannak a modellben. Az iteráció első lépéseként végzett számításban az összes HR elem a hossza mentén egyetlen normál végeselemként szerepel, amely mind a húzó-, mind a nyomó igénybevételnek ellenáll. Ezután a nyomóerővel terhelt HR elemek tengelyirányú szabadságfoka (Ux) felszabadításra kerül, és a számítás, ezzel a módosított modellel újra lefut. Ez az iteratív eljárás addig tart, amíg egyik HR elem állapota sem változik tovább (vagyis nem válik húzottból nyomottá, vagy fordítva). Ha az iteráció nem vezet eredményre, mert 1000 lépésben sem éri el a modell a végső állapotát, akkor az eljárás egy kis módosítással kezdődik elölről. Ebben a következő fordulóban a nyomottá vált HR elemeket minden iterációs lépésben egy fiktív névleges merevséggel (E*A/L/50) helyettesítjük, amíg az első fordulóhoz hasonlóan el nem érjük a stabil modellállapotot. A sajátérték számítás erre a módosított végeselem modellre kerül elvégzésre.
Mivel a sajátérték számítás nem hajtható végre iteratív módon, a fenti stratégia nem alkalmazható. A Consteel ehelyett a sajátértékszámításhoz figyelembe veendő teherkombinációra elvégez egy fenti stratégia szerinti analízist, majd a HR rudakra kapott végeredmény szerinti merevséggel (ténylegesen húzott rúd teljes érték, nominálisan nyomott HR rúd fiktív érték) végzi a sajátértékszámítást. hasonlóan problémás a dinamikai számítás HR rudak esetén. Ebben az esetben a sajátértékekhez használt stratégia sem használható. a Consteel minden HR rudat húzott-nyomott rúdként feltételez, de 50% merevséggel. Ez az érték annak a feltételezésével lett felvéve, hogy jellemzően húzott rudas merevítések párban vannak használva és egy adott terhelésben jellemzően csak az egyik “dolgozik” közülük.